前言

在学习大模型训练库unsloth时看到和FlashAttention的对比，因为之前也听说过，感觉这个技术还挺火的，所以趁这个机会研究一下。

现今的模型基本上基于transformer，模型变的越来越大，越来越深，但是扩展序列长度却还是很困难。因为其核心自注意力模块的内存和时间复杂度对于序列长度是平方级别的。

在FlashAttention之前，业界的主流方案是减少计算量，而没有关注内存的访问成本。现今的显卡的计算速度已经远超内存速度，内存访问已经成为瓶颈。FlashAttention通过减少显存数据的读写量，提高了数据的吞吐量，从而提升速度并节省了内存。

FlashAttention

架构

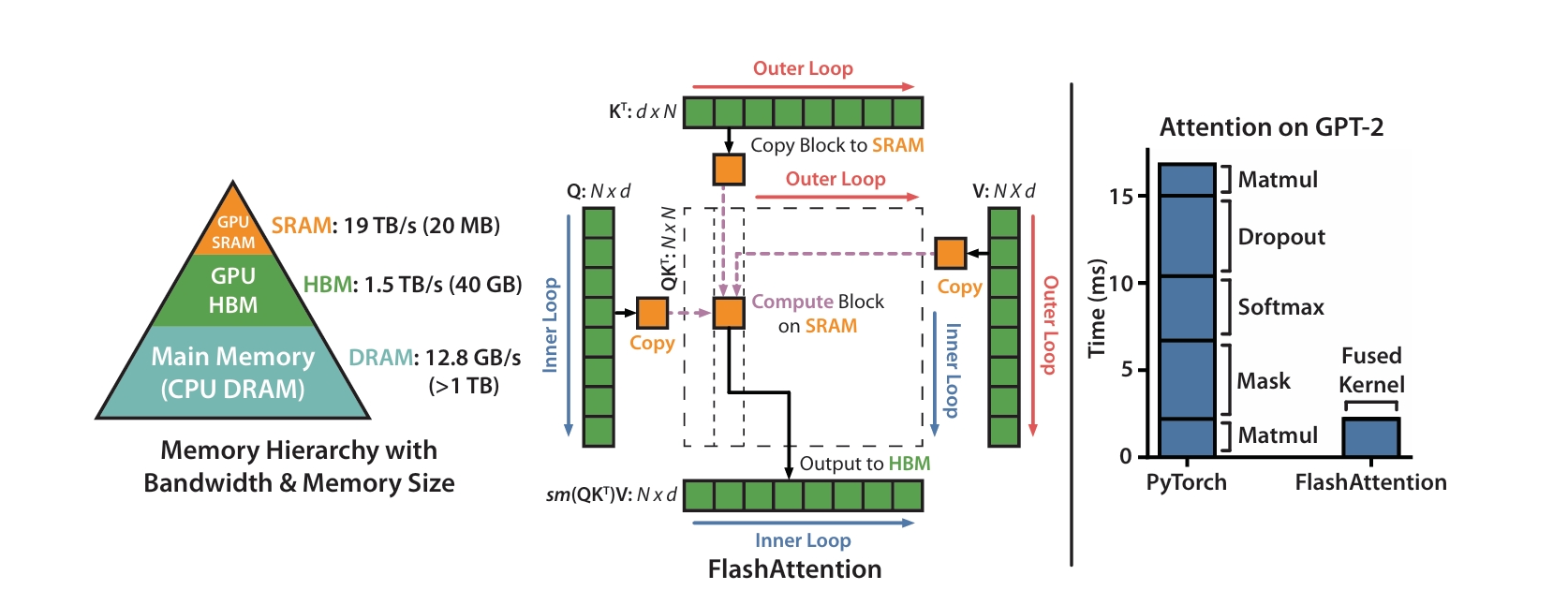
FlashAttention主要使用以下两个技巧：分片计算和重计算。分片计算是指对矩阵进行分片，实现了softmax的分片计算，在前向和后向传播中都使用了分片计算，它使分片后的数据大小能够适应共享内存。重计算是指在前向传播减少存储的数据，在反向传播时计算原先需要的数据。两者的目的都是减少高速内存的访问，尽可能利用共享内存提速。

性能

根据官方提供的数据，和原始Pytorch版本相比，在训练上，FlashAttention的速度至少提升了2倍，FlashAttention2的速度至少提升了3倍。内存减少量随着序列长度线性增长，当序列长度为2k时，内存减少了10倍，当序列长度为4k时，减少了20倍，这个结果说明FlashAttention能使用更长的序列长度。

分片计算

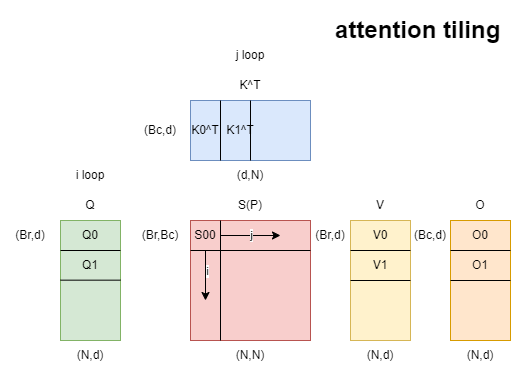
首先为了数值稳定性，引入safe softmax。定义softmax的向量$x\in R^B$，公式如下：

$m(x) = max(x_i), f(x)=[e^{x_1-m(x)} ... e^{x_B-m(x)}], l(x)=\sum_if(x)_i, softmax(x)=\frac{f(x)}{l(x)}$

safe softmax的标准实现：

for i = 1, N do

$m_i=\max(x_{i-1}, x_i)$

end

for i = 1, N do

$l_i=l_{i-1} + e^{x_i-m_N}$

end

for i = 1, N do

$p=softmax(x)=\frac{e^{x_i-m_N}}{l_N}$

end

我们可以看到标准实现使用了三重循环，效率太低。我们可以通过实现softmax的分片计算，实现迭代，减少循环次数。

$\begin{aligned} l_i &= \sum_{j=1}^ie^{x_j-m_i} \\ &= (\sum_{j=1}^{i-1}e^{x_j-m_i}) + e^{x_i-m_i} \\ &= (\sum_{j=1}^{i-1}e^{x_j-m_{i-1}})e^{m_{i-1}-m_i} + e^{x_i-m_i} \\ &= l_{i-1}e^{m_{i-1}-m_i} + e^{x_i-m_i} \end{aligned}$

优化后从三重循环变成双重训练。

for i = 1, N do

$\begin{aligned} m_i&=\max(x_{i-1}, x_i) \\ l_i&=l_{i-1}e^{m_{i-1}-m_i} + e^{x_i-m_i} \end{aligned}$

end

for i = 1, N do

$p_i=softmax(x)=\frac{e^{x_i-m_N}}{l_N}$

end

接下来再看注意力公式，能否将循环次数优化到一次。（为了方便理解，忽略了缩放系数$\frac{1}{\sqrt d}$）

$S=QK^T \in R^{N \times N}, P=softmax(S) \in R^{N \times N}, O=PV \in R^{N \times d}$

设$Q[k,:]$为Q矩阵的第k行向量，$K^T[:,i]$为K矩阵的第i列向量，$O[k,:]$为输出O矩阵的第k行，$V[i,:]$为V矩阵的第i行，$o_i=\sum_{j=1}^ip_jV[j,:]$为分片输出。

for i = 1, N do

$\begin{aligned} x_i&=Q[k,:]K^T[:,i] \\ m_i&=\max(m_{i-1}, x_i) \\ l_i&=l_{i-1}e^{m_{i-1}-m_i} + e^{x_i-m_i} \end{aligned}$

end

for i = 1, N do

$\begin{aligned} p_i&=softmax(x)=\frac{e^{x_i-m_N}}{l_N} \\ o_i&=o_{i-1} + p_iV[i,:] \end{aligned}$

end

$O[k,:]=o_N$

第二个循环依赖了$m_N$和$l_N$，因为$m_N$需要等第一个循环结束才能得到，所以无法直接合并两个循环。但是我们可以借鉴softmax迭代的技巧，实现$o$的迭代。

$\begin{aligned} o_i &=\sum_{j=1}^i\frac{e^{x_j-m_i}}{l_i}V[j,:] \\ &=\sum_{j=1}^{i-1}\frac{e^{x_j-m_i}}{l_i}V[j,:] + \frac{e^{x_i-m_i}}{l_i}V[j,:] \\ &=(\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{l_{i-1}}\frac{l_{i-1}e^{m_{i-1}-m_i}}{l_i}V[j,:]) + \frac{e^{x_i-m_i}}{l_i}V[j,:] \\ &=o_{i-1}\frac{l_{i-1}e^{m_{i-1}-m_i}}{l_i} + \frac{e^{x_i-m_i}}{l_i}V[j,:] \end{aligned}$

优化后的公式只依赖$l_i$，$l_{i-1}$，$m_i$，$m_{i-1}$，$l_i$，因此我们可以合并两个循环。

for i = 1, N do

$\begin{aligned} x_i&=Q[k,:]K^T[:,i] \\ m_i&=\max(m_{i-1}, x_i) \\ l_i&=l_{i-1}e^{m_{i-1}-m_i} + e^{x_i-m_i} \\ o_i&=o_{i-1}\frac{l_{i-1}e^{m_{i-1}-m_i}}{l_i} + \frac{e^{x_i-m_i}}{l_i}V[j,:] \end{aligned}$

end

$O[k,:]=o_N$

最终我们省去了S和P，又因为$x_i,m_i,l_i,o_i$因为占用空间足够小，所以可以放入GPU的共享内存。共享内存的速度比显存高出一个数量级。

重计算

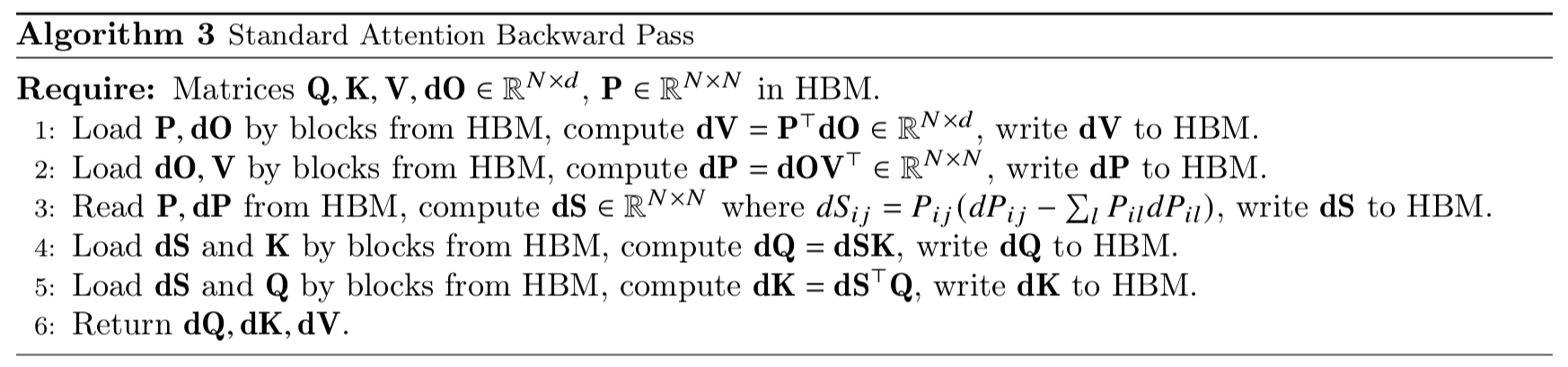
在前向传播中我们省去了S和P，但是反向传播中需要使用S和P，通过在前向传播中引入的m和l，再加上输入Q，K，V，我们可以重新计算得到S和P。

反向传播中，设$\phi$为损失函数，输出梯度$dO=\frac{\partial \phi}{\partial O} \in R^{N \times d}$，需要计算输入梯度$dQ,dK,dV \in R^{N \times d}$。

$q_i$和$k_j$分别表示Q的第i个块和K的第j个块，定义：

$Li=\sum_j e^{q_ik_j^T}$

$v_j$表示V的第j个块，则第i个块的输出：

$o_i=P_{i:}V=\sum_j P_{ij}v_j=\sum_j \frac{e^{q_ik_j^T}}{L_i}v_j$

dP和dV比较简单，可以直接得出，因为$dV=P^TdO$，可得：

$dv_j=\sum_i P_{ij}o_i=\sum_i \frac{e^{q_ik_j^T}}{L_i}do_i$

因为$dP=dOV^T$，可得：

$dP_{ij}=do_iv_j^T$

dQ和dK比较复杂，我们先计算dS。因为$P_{i:}=softmax(S_{i:})$，可以得到以下两个公式：

• $\frac{\partial \phi}{\partial s_{i:}}=\frac{\partial \phi}{\partial p}\frac{\partial p}{\partial s}=dp_{i:}(diag(p_{i:}) - p_{i:}^Tp_{i:})$
• $\frac{\partial \phi}{\partial s_{ij}}=p_{ij}(dp_{ij} - \sum_j p_{ij}dp_{ij})$

pdp的空间复杂度是$O(N^2)$，可能无法一次写入显卡的共享内存，所以论文通过一系列转换将空间复杂度减少到$O(d^2)$（通常$N\gg d$，如N是1K、2K，d是64、128）。

$\begin{aligned} dS_{i:} &=dP_{i:}(diag(P_{i:}) - P_{i:}^TP_{i:}) \\ &=P_{i:} \odot dP_{i:} - (dP_{i:}P_{i:}^T)P_{i:} \\ D_i&=dP_{i:}P_{i:}^T=\sum_j do_iv_j^T\sum_j \frac{e^{q_ik_j^T}}{Li}=do_i\sum_j v_j^T\frac{e^{q_ik_j^T}}{Li}=do_i\sum_j (\frac{e^{q_ik_j^T}}{Li}v_j)^T=do_io_i^T \\ dS_{i:} &=P_{i:} \odot dP_{i:} - D_iP_{i:} \\ dS_{ij} &=P_{ij}dP_{ij} - P_{ij}Di=P_{ij}(dP_{ij} - D_i) \end{aligned}$

有了$S_{ij}$，我们可以算出dQ和dK:

$\begin{aligned} dq_i&=\sum_j dS_{ij}k_j \\ dk_j&=\sum_i dS_{ij}^Tq_i \end{aligned}$

FlashAttention2

FlashAttention2在FlashAttention的基础上优化了3点：

• 算法优化，包括前向和反向传播
• 并行化
• warp之间的工作划分

算法

论文举了一个例子，A100的GPU在执行矩阵操作时的吞吐量理论峰值是312TFLOPs/s，而非矩阵操作的吞吐量是19.5TFLOPs/s。换句话说，非矩阵操作的成本相当于矩阵操作的16倍。所以要尽可能减少非矩阵操作。

前向传播

为了减少非矩阵操作做了2点小调整。

1. 计算注意力输出时，在循环过程中没有必要每次都缩放，而是在最后一步缩放。

2. 不需要再保存为了反向传播重计算用到的m和l，而是保存logsumexp $L=m+log(l)$。（为什么是这个形式在后面的反向传播里解释）

优化后的算法伪代码：

for i = 1, N do

$\begin{aligned} x_i&=Q[k,:]K^T[:,i] \\ m_i&=\max(m_{i-1}, x_i) \\ l_i&=l_{i-1}e^{m_{i-1}-m_i} + e^{x_i-m_i} \\ o_i&=o_{i-1}l_{i-1}e^{m_{i-1}-m_i} + e^{x_i-m_i}V[j,:] \end{aligned}$

end

$L_N=m_N+\log(l_N)$

$O[k,:]=\frac{o_N}{l_N}$

反向传播

使用前向传播保存的logsumexp代替原先的m和l。

$\begin{aligned} P_i &=e^{S_{ij}-L_i} \\ &=e^{S_{ij}-m_i-\log(l_i)} \\ &=\frac{e^{S_{ij}-m_i}}{l_i} \end{aligned}$

经过转换后的P和原先的P相同。

并行化

在FlashAttention中的并行化是基于batch size和注意力头数量。总共需要的线程数是batch size和注意力头数的乘积。当这个数值足够大时，显卡资源利用率是高效的。但是当遇到长seqlen场景时，通常来说batch size和注意力头的数量会小的多，显卡资源的利用率就会降低。这时候就需要对seqlen维度做并行化。

前向传播

FlashAttention中的内层循环对$O_i,m_i,l_i$进行重复读写，为了减少IO访问，可以交换内外层循环的顺序。

反向传播

反向传播维持原样，不需要做调整。因为如果交换了内外层循环，会导致需要通信的变量会增加，从原来的$dQ$变成$dK$和$dV$。

总结，前向传播是以行方向的seqlen做并行，反向传播是以列方向的seqlen做并行。

warp之间的工作划分

先介绍一下什么是warp，在 NVIDIA 的 CUDA 架构中，warp 是由 32 个并行线程组成的执行单元。所有这 32 个线程同时执行相同的指令（SIMT，即单指令多线程），但是它们可以操作不同的数据。通常1个线程有4个或者8个warps。

从论文中的解释可以发现本质是因为第二点的并行化优化减少了IO操作，所以不多做解释。

参考

• FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness (opens new window)
• From Online Softmax to FlashAttention (opens new window)
• CUDA编程入门之激活函数Softmax (opens new window)
• 图解大模型计算加速系列：FlashAttention V1，从硬件到计算逻辑 (opens new window)
• FlashAttention (opens new window)
• FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning (opens new window)