前言

在学习llama模型的训练过程中发现强化学习除了PPO(proximal policy optimization)还有一个DPO可选项(direct preference optimization)，在我的上一篇笔记里有提到两本入门课程（Easy RL和动手学强化学习）里并没有提到这个算法，应该是最近新出现的，查了一下该算法是在23年提出的。

在学习DPO之前，我们先回顾一下RLHF。

RLHF（人类反馈的强化学习）

While large-scale unsupervised language models (LMs) learn broad world knowledge and some reasoning kills, achieving precise control of their behavior is difficult due to the completely unsupervised nature of their training. Existing methods for gaining such steerability collect human labels of the relative quality of model generations and fine-tune the unsupervised LM to align with these preferences, often with reinforcement learning from human feedback (RLHF). However, RLHF is a complex and often unstable procedure, first fitting a reward model that reflects the human preferences, and then fine-tuning the large unsupervised LM using reinforcement learning to maximize this estimated reward without drifting too far from the original model.

虽然大规模的无监督语言模型能够可以学习广泛的世界知识和一些推理技能，但由于其训练完全是无监督的，要精确控制它们的行为是很困难的。为了获得这种可操控性，现有的方法收集人类对模型生成内容相对质量的标签，并利用这些偏好对无监督的语言模型进行微调，常常使用基于人类反馈的强化学习（RLHF）。然而，基于人类反馈的强化学习（RLHF）是一个复杂且常常不稳定的过程。首先需要构建一个反映人类偏好的奖励模型，然后利用强化学习对大型无监督语言模型进行微调，以最大化这一估计的奖励，同时又不会使模型偏离其原始状态太远。这个过程涉及多个挑战，包括如何准确捕捉和量化人类的偏好，以及如何在增强预期性能的同时保持模型的原始知识和功能。

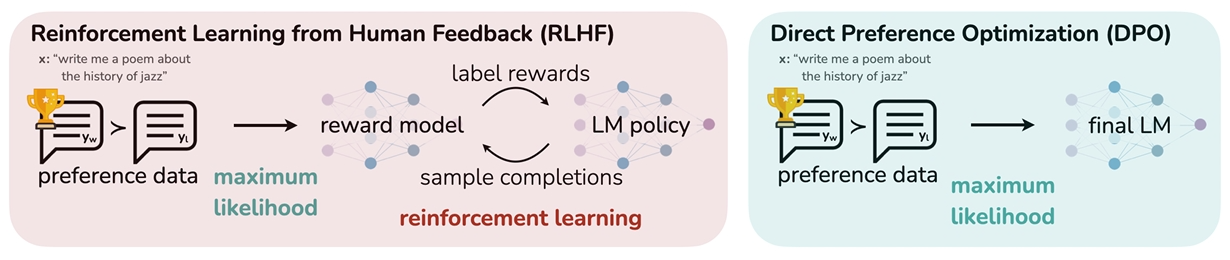
论文中给出的图片总结了RLHF和DPO的训练流程。

RLHF分为3个阶段：

1. 微调（SFT）
2. 奖励模型（RM）
3. 强化学习（RL）

RLHF训练过程涉及4个模型，分别是奖励模型、ref模型、actor模型、critic模型，训练流程相当复杂。在强化学习（RL）阶段，需要在训练循环中采样，计算成本高。

DPO（直接偏好优化）

In this paper we introduce a new parameterization of the reward model in RLHF that enables extraction of the corresponding optimal policy in closed form, allowing us to solve the standard RLHF roblem with only a simple classification loss. The resulting algorithm, which we call Direct Preference Optimization (DPO), is stable, performant, and computationally lightweight, eliminating he need for sampling from the LM during fine-tuning or performing significant hyperparameter tuning. Our experiments show that DPO can fine-tune LMs to align with human preferences as well as or better than existing methods. Notably, fine-tuning with DPO exceeds PPO-based RLHF in ability to control sentiment of generations, and matches or improves response quality in summarization and single-turn dialogue while being substantially simpler to implement and train.

在这篇论文中，我们引入了一种新的奖励模型参数化方法，用于基于人类反馈的强化学习（RLHF），该方法使得相应的最优策略能以封闭形式被提取出来，允许我们仅使用简单的分类损失来解决标准的RLHF问题。我们将这一算法称为直接偏好优化（Direct Preference Optimization, DPO），它稳定、高效且计算成本低，无需在微调过程中从语言模型（LM）进行抽样或进行大量的超参数调整。我们的实验显示，DPO能够微调语言模型以符合人类偏好，其效果与现有方法相当或更优。值得注意的是，与基于PPO的RLHF相比，使用DPO进行微调在控制生成内容的情感方面表现更佳，并且在摘要和单轮对话的响应质量方面达到或超过现有水平，同时实现和训练过程也大为简化。

先说最直观的结果，DPO基于PPO优化掉了奖励模型（RM）和强化学习（RL），使用偏好数据从微调（SFT）直接到最终模型。模型数量从4个优化到了2个。

准备工作

因为DPO是基于PPO优化而来，所以我们先回顾一下PPO的流程。

微调模型：我们通过微调预训练模型得到一个模型记为$\pi^{SFT}$。

奖励模型：微调模型根据我们提供的提示$x$生成答案对$(y_1,y_2)\sim\pi^{SFT}(y|x)$。这些答案对经过人工标注后得到人类的偏好数据，表示为$y_w\succ y_l|x$，其中$y_w$和$y_l$分别表示偏好的和不偏好的答案。这些偏好被假设为由某个潜在的奖励模型$r^*(x,y)$生成，不过我们并不会直接使用这个模型。对于偏好建模有很多种方法，论文中使用的是Bradley-Terry（BT）模型。根据BT模型规定，人类偏好分布$p^*$可以表示为：

$p^*(y_1\succ y_2|x)=\frac{exp(r^*(x,y1))}{exp(r^*(x,y1))+exp(r^*(x,y2))}$

假设有数据集$D=\{x^{(i)},y_w^{(i)},y_l^{(i)}\}_{i=1}^N$，采样于分布$p^*$，我们可以参数化奖励模型$r_\phi(x,y)$，通过最大似然估计参数。将问题转化为二分类问题，我们得到负对数似然损失：

$L_R(r_\phi,D)=-E_{(x,y_w,y_l)\sim{D}}[\log\sigma(r_\phi(x,y_w)-r_\phi(x,y_l))]$

$\sigma$是sigmoid函数。

强化学习：我们使用训练过的奖励函数为语言模型提供反馈，构建以下优化问题：

$\displaystyle\max_{\pi_\theta}E_{x\sim D,y\sim \pi_\theta(y|x)}[r_\phi(x,y)]-\beta D_{KL}[\pi_\theta(y|x)||\pi_{ref}(y|x)]$

$\beta$作为参数控制策略$\pi_\theta$相对于基础参考策略$\pi_{ref}$的偏移。后一项是KL散度，作为惩罚项，防止模型偏离基础参考模型太多，同时它保证了生成内容的多样性，防止了模型崩塌到单一的高奖励答案。

推导DPO的优化目标

我们继续推导上面一节强化学习的公式，首先展开KL散度项合并到期望公式，第二步将max转为min，最后合并两项。

KL散度公式：$D_{KL}[\pi_\theta(y|x)||\pi_{ref}(y|x)]=\displaystyle\sum_{i=1}^N\pi_\theta(y|x)\log\frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)}=E_{x\sim D,y\sim \pi(y|x)}(\log\frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)})$

$\begin{aligned} \displaystyle\max_{\pi}E_{x\sim D,y\sim \pi(y|x)}[r(x,y)]-\beta D_{KL}[\pi(y|x)||\pi_{ref}(y|x)] &=\displaystyle\max_{\pi}E_{x\sim D,y\sim \pi(y|x)}[r(x,y)-\beta\log\frac{\pi(y|x)}{\pi_{ref}(y|x)}] \\ &=\displaystyle\min_{\pi}E_{x\sim D,y\sim \pi(y|x)}[\log\frac{\pi(y|x)}{\pi_{ref}(y|x)}-\frac{1}{\beta}r(x,y)] \\ &=\displaystyle\min_{\pi}E_{x\sim D,y\sim \pi(y|x)}[\log\frac{\pi(y|x)}{\frac{1}{Z(x)}\pi_{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))}-\log Z(x)] \end{aligned}$

$Z(x)$是配分函数（partition function）。

$Z(x)=\displaystyle\sum_y \pi_{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$

什么是配分函数？它是统计物理学中的一个概念，我们可以简单理解为它用来确保概率总和为1。

因为有了配分函数，我们定义一个新的策略分布：

$\pi^*(y|x)=\frac{1}{Z(x)}\pi_{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$

因为$\pi^*>=0$并且对于所有的y有$\sum_y \pi^*(y|x)=1$，所以它是一个合法的概率分布。

因为$Z(x)$与y无关，我可以重构公式：

$\displaystyle\min_{\pi}E_{x\sim D}[E_{y\sim \pi(y|x)}[\log\frac{\pi(y|x)}{\pi^*(y|x)}]-\log Z(x)]=\displaystyle\min_{\pi}E_{x\sim D}[D_{KL}[\pi(y|x)||\pi^*(y|x)]-\log Z(x)]$

因为$Z(x)$不依赖于$\pi$，所以最小值只看KL散度项。根据吉布斯不等式（Gibbs' inequality），KL散度要取到最小值有且只有当两个分布相同时。于是我们可以得到最优解：

$\pi(y|x)=\pi^*(y|x)=\frac{1}{Z(x)}\pi_{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$

转换上面的公式，我们可以得到：

$r^*(x,y)=\beta\log\frac{\pi^*(y|x)}{\pi_{ref}(y|x)}+\beta\log Z(x)$

将上面公式代入BT模型的人类偏好概率分布公式，我们可以得到：

$\begin{aligned} p^*(y_1\succ y_2|x) &=\frac{exp(\beta\log\frac{\pi^*(y_1|x)}{\pi_{ref}(y_1|x)}+\beta\log Z(x))}{exp(\beta\log\frac{\pi^*(y_1|x)}{\pi_{ref}(y_1|x)}+\beta\log Z(x))+exp(\beta\log\frac{\pi^*(y_2|x)}{\pi_{ref}(y_2|x)}+\beta\log Z(x))} \\ &=\frac{1}{1+exp(\beta\log\frac{\pi^*(y_2|x)}{\pi_{ref}(y_2|x)}-\beta\log\frac{\pi^*(y_1|x)}{\pi_{ref}(y_1|x)})} \\ &=\sigma(\beta\log\frac{\pi^*(y_2|x)}{\pi_{ref}(y_2|x)}-\beta\log\frac{\pi^*(y_1|x)}{\pi_{ref}(y_1|x)}) \end{aligned}$

配分函数被抵消了，我们可以只用最优策略$\pi^*$和参考策略$\pi_{ref}$来表示人类偏好概率，不再需要奖励模型。我们可以参数化策略$\pi_\theta$得到最大似然目标：

$L_{DPO}(\pi_\theta;\pi_{ref})=-E_{(x,y_w,y_l)\sim D}[\log\sigma(\beta\log\frac{\pi^*(y_w|x)}{\pi_{ref}(y_w|x)}-\beta\log\frac{\pi^*(y_l|x)}{\pi_{ref}(y_l|x)})]$

DPO使用一种替代的参数化方法来拟合一个隐式的奖励函数，其最优策略简单地表示为$\pi_\theta$，成功绕过了奖励模型和强化学习。

我们继续看一下损失函数的梯度。

$\begin{aligned} u=\beta\log\frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)}-\beta\log\frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)} \\ \nabla_\theta L_{DPO}(\pi_\theta;\pi_{ref})=-E_{(x,y_w,y_l)\sim D}[\frac{\sigma'(u)}{\sigma(u)}\nabla_\theta u] \end{aligned}$

根据sigmoid函数的导数可知$\sigma'(u)=(1-\sigma(u))\sigma(u)$，且$\sigma(-u)=1-\sigma(u)$。

$\begin{aligned} \nabla_\theta L_{DPO}(\pi_\theta;\pi_{ref}) &=-E_{(x,y_w,y_l)\sim D}[\sigma(-u)\nabla_\theta u] \\ &=-E_{(x,y_w,y_l)\sim D}[\beta\sigma(\beta\log\frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)}-\beta\log\frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)})[\nabla_\theta\log\pi(y_w|x)-\nabla_\theta\log\pi(y_l|x)]] \\ &=-\beta E_{(x,y_w,y_l)\sim D}[\sigma(\hat r_\theta(x,yl)-\hat r_\theta(x,y_w))[\nabla_\theta\log\pi(y_w|x)-\nabla_\theta\log\pi(y_l|x)]] \end{aligned}$

$\hat r_\theta(x,y)$是由策略$\pi_\theta$和$\pi_{ref}$定义的隐式奖励函数。要使损失最小化，就要减少梯度，因为负号的关系，实际要使策略梯度的差值为正，也就是说需要增加策略梯度$\nabla_\theta\log\pi(y_w|x)$，减少策略梯度$\nabla_\theta\log\pi(y_l|x)$。所以损失函数的梯度会增加偏好$y_w$的可能性，减少非偏好$y_l$的可能性。中间的权重项的含义是隐式奖励模型对偏好和非偏好答案的排序结果的错误系数，它作为惩罚项，类似PPO中的KL散度，防止模型退化。

参考

• Direct Preference Optimization: Your Language Model is Secretly a Reward Model (opens new window)
• Bradley-Terry 模型 (opens new window)
• 配分函数 (opens new window)
• 吉布斯不等式 (opens new window)