位置编码

在处理词元序列时，自注意力机制因为并行计算而放弃了顺序操作，模型在学习过程中虽然可以捕获不同元素之间的关系，但是无法得知各种元素之间的相对位置信息。为了解决这个问题，位置编码被引入，为模型提供关于元素在序列中位置的信息。

正弦余弦位置编码

transformers使用了正弦和余弦的位置编码。

用i表示词元在序列中的位置，d表示编码维度，使用成对的正弦和余弦函数,2j表示偶数维度，2j+1表示奇数维度（要求d是偶数）。

$\begin{array}{c} p_{i,2j}=sin(\frac{i}{10000^\frac{2j}{d}}) \\ p_{i,2j+1}=cos(\frac{i}{10000^\frac{2j}{d}}) \end{array}$

为什么使用成对的正弦和余弦函数，只使用正弦或者余弦可行吗？只使用正弦或者余弦会无法捕捉不同词元间的相对位置，同时使用正弦余弦可以使模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移$\delta$，位置i+$\delta$的位置编码可以由位置i的位置编码通过线性变换得到。

$\begin{aligned} &\left[ \begin{matrix} cos(\delta x_j) & sin(\delta x_j) \\ -sin(\delta x_j) & cos(\delta x_j) \end{matrix} \right] \left[ \begin{matrix} p_i,_{2j} \\ p_i,_{2j+1} \end{matrix} \right] \\ &= \left[ \begin{matrix} cos(\delta x_j)sin(ix_j) + sin(\delta x_j)cos(ix_j) \\ -sin(\delta x_j)sin(ix_j) + cos(\delta x_j)cos(ix_j) \end{matrix} \right] \\ &= \left[ \begin{matrix} sin((\delta+i)x_j) \\ cos((\delta+i)x_j) \end{matrix} \right] \\ &= \left[ \begin{matrix} p_{i+\delta,2j} \\ p_{i+\delta,2j+1} \end{matrix} \right] \end{aligned}$

代码实现，参考了d2l的实现。

class PositionalEncoding(nn.Module):
    def __init__(self, num_hiddens, dropout, max_len=1000):
        super().__init__()
        self.dropout = nn.Dropout(dropout)
        # Create a long enough P
        self.P = d2l.zeros((1, max_len, num_hiddens))
        X = d2l.arange(max_len, dtype=torch.float32).reshape(
            -1, 1) / torch.pow(10000, torch.arange(
            0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)   # 偶数位
        self.P[:, :, 1::2] = torch.cos(X)   # 奇数位

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

旋转位置编码

旋转位置编码在正弦余弦位置编码的基础上做了优化，将模型需要学习才能得到词元间的相对位置信息前置到注意力计算阶段。

注意力计算公式：

$Attention(Q,K,V)=softmax(\frac{Q^TK}{\sqrt d})V$

需要找到一个函数f，要求满足以下性质：

1. 容易和注意力公式结合，即乘法表示。
2. 不能满足交换律，例如”我爱你“和”你爱我“的含义是不同的。
3. 距离衰减，距离较近的词元乘积更大，较远的乘积更小。
4. 良好的外推性，对于超过限制长度的样本，模型性能不会受损。

矩阵乘法满足以上性质，接下来需要找到矩阵R，使其满足公式：

$R_{m-n}=R_m^TR_n$

将公式(4)和注意力计算公式结合可以得出以下公式：

$R_{m-n}q^Tk=(R_mq)^T(R_nk)$

根据公式(2)可知在二维形式下矩阵R如下：

$\left[ \begin{matrix} cos(m\theta) & -sin(m\theta) \\ sin(m\theta) & cos(m\theta) \end{matrix} \right]$

推广到多维形式：

$R^d= \left[ \begin{matrix} cos(m\theta_0) & -sin(m\theta_0) & 0 & 0 & ... & 0 & 0 \\ sin(m\theta_0) & cos(m\theta_0) & 0 & 0 & ... & 0 & 0 \\ 0 & 0 & cos(m\theta_1) & -sin(m\theta_1) & ... & 0 & 0 \\ 0 & 0 & sin(m\theta_1) & cos(m\theta_1) & ... & 0 & 0 \\ ... & ... & ... & ... & ... & ... & ... \\ 0 & 0 & 0 & 0 & ... & cos(m\theta_{d/2-1}) & -sin(m\theta_{d/2-1}) \\ 0 & 0 & 0 & 0 & ... & sin(m\theta_{d/2-1}) & cos(m\theta_{d/2-1}) \\ \end{matrix} \right] \left[ \begin{matrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ ... \\ q_{d-2} \\ q_{d-1} \\ \end{matrix} \right]$

$\theta=\{\theta_i=10000^{-2(i-1)/d},i\epsilon[1,2,...,d/2]\}$

因为矩阵中存在大量的0，为了减少计算量，可以改为以下公式，等价于公式(6):

$R^d= \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ ... \\ q_{d-2} \\ q_{d-1} \\ \end{bmatrix} \otimes \begin{bmatrix} cos(m\theta_0) \\ cos(m\theta_1) \\ cos(m\theta_2) \\ cos(m\theta_3) \\ ... \\ cos(m\theta_{d/2-1}) \\ cos(m\theta_{d/2-1}) \\ \end{bmatrix} + \begin{bmatrix} -q_1 \\ q_0 \\ -q_3 \\ q_2 \\ ... \\ -q_{d-1} \\ q_{d-2} \\ \end{bmatrix} \otimes \begin{bmatrix} sin(m\theta_0) \\ sin(m\theta_1) \\ sin(m\theta_2) \\ sin(m\theta_3) \\ ... \\ sin(m\theta_{d/2-1}) \\ sin(m\theta_{d/2-1}) \\ \end{bmatrix}$

下图直观的描绘了位置编码旋转的过程。

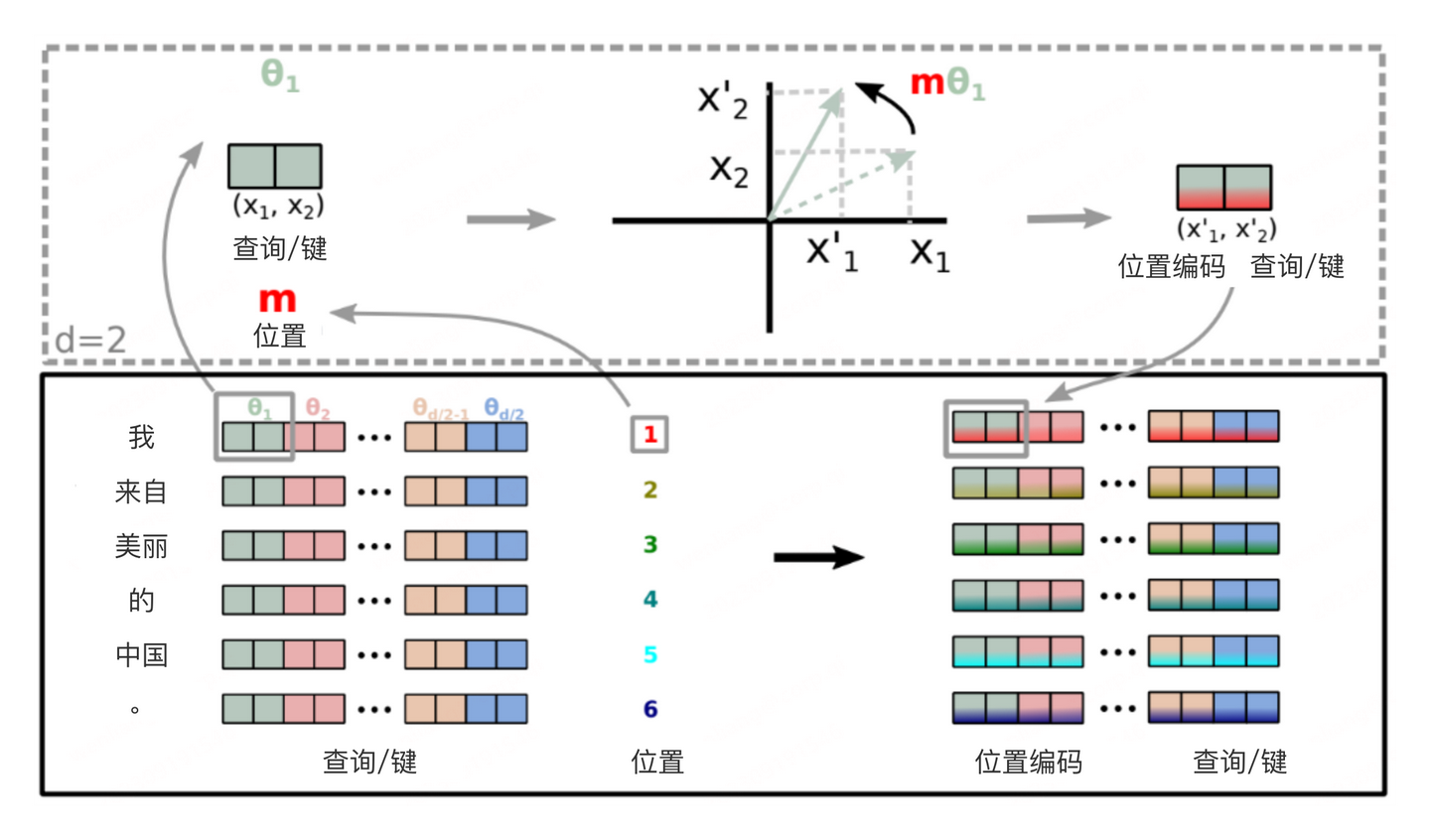
为什么被称为旋转位置编码的原因是矩阵R被称为旋转矩阵。参考上图中的平面坐标轴，存在点x1 $(x_1,y_1)$，点x2 $(x_2,y_2)$，斜边长r，角度$\theta$、$\gamma$，推导公式如下：

$y_1=rsin(\theta)$

$x_1=rcos(\theta)$

$y_2=rsin(\theta+\gamma)$

$x_2=rcos(\theta+\gamma)$

$x_2=r(cos(\theta)cos(\gamma) - sin(\theta)sin(\gamma))=x_1cos(\theta)-y_1sin(\theta)$

$y_2=r(sin(\theta)cos(\gamma) - cos(\theta)sin(\gamma))=x_1sin(\theta)-y_1cos(\theta)$

$\begin{bmatrix} x_2 \\ y_2 \end{bmatrix} = \begin{bmatrix} cos(m\theta) & -sin(m\theta) \\ sin(m\theta) & cos(m\theta) \end{bmatrix} \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}$

矩阵R乘上点x1相当于绕原点逆时针旋转了角度$\theta$。

代码实现，参考了huggingface的实现，只保留关键代码。

class LlamaAttention(nn.Module):
    def __init__(self, config: LlamaConfig, layer_idx: Optional[int] = None):
        super().__init__()
        self.config = config
        self.layer_idx = layer_idx
        self.hidden_size = config.hidden_size
        self.num_heads = config.num_attention_heads
        self.head_dim = self.hidden_size // self.num_heads
        self.max_position_embeddings = config.max_position_embeddings
        self.rotary_emb = LlamaRotaryEmbedding(
            self.head_dim,
            max_position_embeddings=self.max_position_embeddings,
            base=self.rope_theta,
        )
    def forward(
        self,
        hidden_states: torch.Tensor,
        attention_mask: Optional[torch.Tensor] = None,
        position_ids: Optional[torch.LongTensor] = None,
    ):
        # 应用旋转位置编码
        cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)
        query_states, key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin, position_ids)
        # 注意力计算
        attn_weights = torch.matmul(query_states, key_states.transpose(2, 3)) / math.sqrt(self.head_dim)

def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., 0::2]
    x2 = x[..., 1::2]
    return torch.cat((-x2, x1), dim=-1)

def apply_rotary_pos_emb(q, k, cos, sin, position_ids, unsqueeze_dim=1):
    """Applies Rotary Position Embedding to the query and key tensors."""
    cos = cos[position_ids].unsqueeze(unsqueeze_dim)
    sin = sin[position_ids].unsqueeze(unsqueeze_dim)
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed

class LlamaRotaryEmbedding(nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
        super().__init__()

        self.dim = dim
        self.max_position_embeddings = max_position_embeddings
        self.base = base
        inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2).float().to(device) / self.dim))
        self.register_buffer("inv_freq", inv_freq, persistent=False)

        # Build here to make `torch.jit.trace` work.
        self._set_cos_sin_cache(
            seq_len=max_position_embeddings, device=self.inv_freq.device, dtype=torch.get_default_dtype()
        )

    def _set_cos_sin_cache(self, seq_len, device, dtype):
        self.max_seq_len_cached = seq_len
        t = torch.arange(self.max_seq_len_cached, device=device, dtype=self.inv_freq.dtype)

        freqs = torch.outer(t, self.inv_freq)
        # Different from paper, but it uses a different permutation in order to obtain the same calculation
        emb = torch.cat((freqs, freqs), dim=-1)
        self.register_buffer("cos_cached", emb.cos().to(dtype), persistent=False)
        self.register_buffer("sin_cached", emb.sin().to(dtype), persistent=False)

    def forward(self, x, seq_len=None):
        # x: [bs, num_attention_heads, seq_len, head_size]
        if seq_len > self.max_seq_len_cached:
            self._set_cos_sin_cache(seq_len=seq_len, device=x.device, dtype=x.dtype)

        return (
            self.cos_cached[:seq_len].to(dtype=x.dtype),
            self.sin_cached[:seq_len].to(dtype=x.dtype),
        )